We’ve all heard people say, “oh you should be more optimistic!”. But honestly, besides having a prettier outlook on life, what’s the point? Doesn’t optimism set us up for disappointment anyways? Why even bother arguing for or against optimism? Why even bother writing a blog post? … Maybe I’m getting a little ahead of myself, since I am writing a blog post. But if you happen to be a computer in a simple randomized experiment, it does make sense to be optimistic, at least in the short term. Am I suggesting we learn life lessons from a textbook? Well I’m not saying I even take my own advice, but maybe yeah.
Chapter 2 of Richard Sutton’s online Reinforcement Learning book is all about action value methods. The basic idea is that you have an agent exploring different actions who is trying to find the best one. Based on the immediate rewards, the agent updates its beliefs on what the best action is to take next. There are several action value methods, like \(\epsilon\)-greedy, reinforcement comparison, softmax, and so on… But in section 2.7, Sutton goes into optimistic initial values, which is a bit striking!
Here’s the setup of the experiment (the 10-armed test bed): You have 10 arms each with different rewards generated from random normal gaussians \(N(0,1)\). The objective of the game is to choose the best arm the most number of times over 1500 plays, to get the most reward. To make the game a little bit harder, we insert random noise $N(0,1)$ into the rewards. There are 2000 different games that we will play, with 1500 plays per game. We can then compare different methods by averaging the rewards over all the games to see which policy does best!
We will have two players, the “Realist” and the “Optimist”. Both the Realist and Optimist will use the \(\epsilon\)-greedy method to explore arms, where \(\epsilon = .1\), the probability of choosing a random arm on each play. If the player doesn’t wind up choosing a random arm, it picks a greedy arm, or the arm with the biggest weighted average of past rewards. Here we use \(\alpha = 0.1\) as the step-size parameter in the update \(Q_{k+1} = Q_k + \alpha (r_{k+1} - Q_k)\), where \(r_{k+1}\) is the reward of the \(k+1\) play and \(Q_k\) is the weighted average of past rewards. Having a constant $\alpha$ is good for problems where the rewards change over time (see Chapter 2.6), although we won’t do that here (but you get similar results).
Here is the crucial part. The Realist starts off with a realistic expectation (duh!), where $Q_0 = 0$ for all arms; $Q_0$ is the initial belief about the reward the player expects from each arm. So $Q_0 = 0$ is pretty realistic!! We know that all the arms were initialized from a gaussian with mean 0, so why should we expect anything different? The Optimist on the other hand, will have different $Q_0$ values. The more $Q_0 > 0$, the more optimistic the Optimist is. If $Q_0 < 0$, the Optimist starts being pessimistic! Oh no!
Let’s cut to the chase! Who does better? In the image below, I show the percent of games that each player chose the best arm for each play. The pessimist on the far left does the worst! The Optimist does better than the Realist during the first 1000 plays or so, but both players find the best arms around 1400 plays (they both converge to just $\epsilon$-greedy). Even more interesting though, is that the more optimistic the Optimist is, the more disappointed the player is with the rewards it’s seeing. So it takes longer for the Optimist to settle on the best arm since it keeps switching. There is of course a sweet spot for just the right amount of optimism that gets the most reward: the Optimist gets disappointed enough to explore more than the realist, but not too disappointed when it finds the best arm (just like Goldilocks). And being a realist ain’t bad, but it isn’t as good as being slightly optimistic…
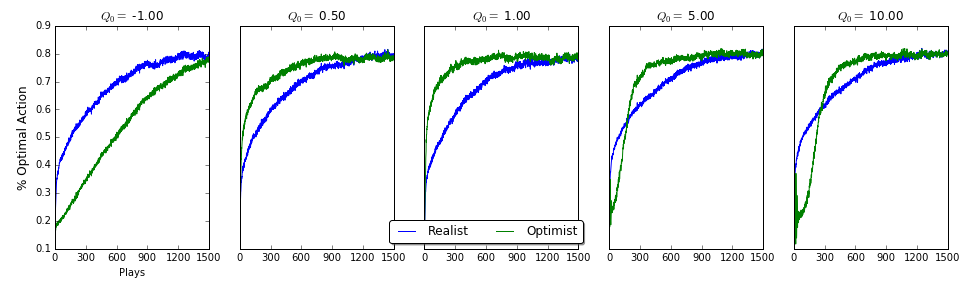
So if life were random gaussians, being an optimist seems like a pretty solid choice; you’ll probably get disappointed, but you’ll keep searching to find the best reward quicker than if you were a pessimist or even a realist. If you’re too optimistic though, you might crash and burn early on, and that doesn’t really help (see image below for average reward per play).
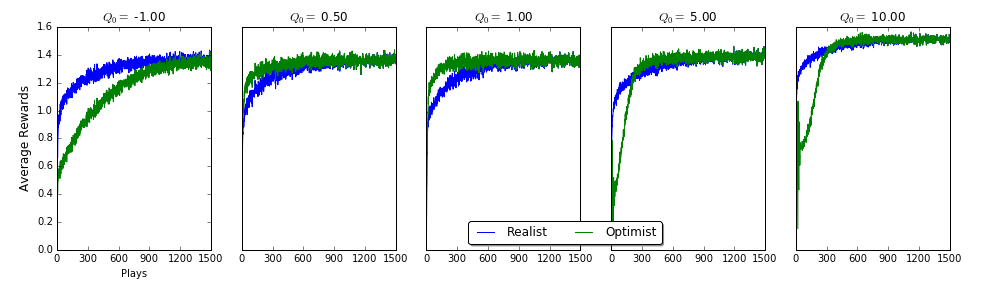
“Ok cool”, you’re probably thinking, “but life isn’t a bunch of random gaussians.” Well, I’ll leave that one up for discussion!
Code is here.